O crescimento econômico é um assunto fascinante, e se você chegou até esse blog é porque provavelmente se deparou com a questão por algum aspecto. Seja qual tenha sido sua motivação, este é um texto que irão introduzi-lo no tema, e lhe fornecerá subsídios suficientes para iniciar uma discussão nesse tema tão debatido dentro e fora das universidades. Este texto que aqui se apresenta é um resumo do livro "Modernas Teorias do Crescimento Econômico - Uma Introdução", de Hywel G. Jones aliado a tópicos do "Manual de Macroeconomia da USP" e do "Macroeconomia" do Mankiw. Aos autores deve-se todas as virtudes do texto, e à mim as possíveis falhas. De qualquer forma, este é um trabalho que objetiva ajudar o estudante de graduação (ou talvez de pós-graduação) a inserir-se na temática do crescimento econômico.
Parafraseando Lucas (1988), quando se pensa no assunto do crescimento econômico, fica difícil pensar em todo o restante. Isto se deve provavelmente ao fato de que o crescimento econômico é algo inerente à vida de praticamente todos os seres humanos. Estamos lidando com a condição de como a riqueza é produzida e distribuída ao longo do tempo, de como as condições de vida dos seres humanos de um ou mais países, estados ou regiões, se alteram ao longo dos anos.
Na teoria econômica este é um assunto antigo e polêmico, cuja discussão se inicia no clássicos do século XIX, mas que ganhará corpo somente no século XX, à luz de fatos como a crise de 29 ou as guerras mundiais que abriram a primeira metade do século. Antes disso, predominavam as "grandes teorias", que abarcavam grandes aspectos das ciências humanas, porém com carência de precisão na análise. Os grandes "economistas clássicos" dos Séculos XVIII e XIX - Smith, Ricardo, Malthus, Mill e, em particular, Marx - foram todos, nesse sentido, "grandes" teoristas. Nos tempos recentes, o celebrado trabalho de Rostow sobre "decolagem para o crescimento sustentável" poderia também ser classificado como uma "grande" teoria. As "grandes" teorias. por sua própria natureza, raramente são precisas. Elas pretendem capturar o todo abrangente do processo histórico do crescimento econômico e do desenvolvimento; e esse objetivo não é, como um todo, compatível com o rigor e com a precisão de uma abordagem mais formal. Os modelos de crescimento econômico têm tido então, principalmente desde a metade do século XX, a matemática como algo intrínseco, como resposta ao caráter analítico que a teoria vem ganhando, principalmente depois da chamada "Revolução Keynesiana". Neste ensaio sobre o assunto, buscaremos minimizar o uso do cálculo e da álgebra linear. Quando isso se fizer impossível, indicaremos outras páginas ou livros que você poderá buscar caso tenha alguma dificuldade.
Jones (1975) coloca que "(...) o interesse contemporâneo por teorias modernas de crescimento econômico pode ser convenientemente datado pela publicação do trabalho original de Harrod (em 1934¹) seguido logo pela contribuição similar, mas originada independentemente de Domar". Sendo assim, um ponto interessante para se iniciar tal estudo, é o modelo de crescimento de Harrod-Domar. Mas antes, é interessante apontar alguns aspectos metodológicos que têm norteado esses modelos.
É comum nas ciências econômicas a crítica de que os economistas são irrealistas quando tratam da analise do mundo, e de que precisariam de mais fatos e menos teorias para fazerem suas colocações. Talvez seja desnecessário dizer que viver somente de fatos é impossível, uma vez que não temos "tantos fatos assim" para aprendermos com eles. Bem como realmente não faz sentido que vivamos somente de teorias. É consenso então que o desenvolvimento científico econômico leve em conta ambas as coisas. Com base nisso, no que tange à teoria do crescimento econômico, Kaldor, na primeira metade do século, desenvolveu um aparato de fatos estilizados a partir do qual deveria se desenvolver uma teoria do crescimento com alguma disciplina, e por mais que fosse por vezes criticados (por Solow e Samuelson por exemplo), esses "fatos" realmente fornecem um esqueleto tosco mas útil para a nossa construção teórica. Listemos os fatos:
1. O crescimento é continuado no volume agregado da produção e na produtividade do trabalho;
2. O crescimento é continuado no montante de capital por trabalhador;
3. A taxa de lucro sobre o capital é constante;
4. A relação "capital-produto" é constante em longos períodos;
5. Há uma alta correlação entre a participação dos lucros na renda e a participação do investimentos no produto; há uma participação constante nos lucros (e salários) em sociedades e/ou períodos nos quais o coeficientes de investimento (a participação do investimento no produto) é constante."
6. Há diferenças substanciais na taxa de crescimento do produto e produtividade do trabalho entre países;
É claro que alguns desses fatos são bem discutíveis, mas em geral, eles nos servem como norte para se iniciar a pesquisa no tema, como veremos mais adiante. Observando algunas dados do mundo real, podemos intuir que os fatos sejam verdadeiros. Se tomarmos por exemplo, o produto per capita, e entendermos a população geral como força de trabalho, podemos ver que a relação tem sido crescente para países emergentes como Brasil, Índia e China (figura 1). Se você se der ao trabalho de testar essa relação para os demais países do mundo verá que ela é verdadeira para a grande maioria.
Mesmo que alguns argumentem que faltam bases sólidas para a construção da teoria do crescimento econômico, e que os fatos na qual ela se baseia são suspeitos, ainda assim podemos dizer que a tentativa de formulação dessa teoria enriquece o pensamento nas ciências humanas, na medida em que se observa a sua importância, como a de se perguntar por que o crescimento chinês nas últimas décadas é tão volumoso, ainda mais quando comparado aos seus colegas do BRIC's.
CONCEITOS E MÉTODOS
É interessante que antes de entrarmos na teoria do crescimento em si, revejamos ou até apresentemos alguns conceitos macroeconômicos essenciais. Basicamente, as diversas teorias do crescimento passarão por esses aspectos com maior ou menor intensidade, mas posso afirmar com certeza que todas passarão. Seja para se afirmar, seja para construir uma antítese do que está sendo dito.
Muito da nomenclatura macroeconômica atual nasce da análise keynesiana, mas não confunda as diversas teorias do crescimento como sendo keynesianas. Elas possuem essas categorias devido à macroeconomia ter ganho corpo na obra de keynes e alguns de seus contemporâneos, mas isso não implica que tudo o que seja dito em macroeconomia seja feito sob a sombra de Keynes. Pra dizer bem a verdade tem bastante coisa na Teoria do Emprego, dos Juros e da Moeda que Keynes podia não ter escrito, mas isso é outro assunto.
Continuando a respeito dos principais conceitos, vamos resumi-los a seguir:
a) Renda ou Produto Nacional
Este é um conceito de fluxo. Se refere à variedade de bens e serviços produzidos numa economia durante qualquer período de tempo (e exatamente por essa última característica é uma variável de fluxo). Corresponde ao total das rendas de todas as firmas e famílias (ou ao total das despesas). Logicamente, medir este agregado não é tarefa fácil, e sua estimativa pelos órgãos governamentais pode apresentar distorções quanto ao produto real. Seja pela questão da oscilação de preços seja por questões estatísticas e metodológicas, por essa razão, essas medidas geralmente são apresentadas em duas formas: preços correntes e preços constantes.
A renda ainda pode ser dividida entre real e potencial. A qualquer instante de tempo certo nível de renda poderia ser gerado se a economia estivesse empregando totalmente todos os fatores disponíveis - isto é, a economia estaria em sua fronteira de produção. No entanto, por diversas razões a economia pode não estar operando em sua capacidade máxima, e logo temos que diferir o que seja o produto real daquilo que ele pode vir a ser, ou seja, o produto potencial. Utilizaremos aqui notação mais comum encontrada em livros de graduação e pós-graduação e definiremos renda como Y, e o produto nacional, quando necessário distinguí-lo, usaremos Q.
b) Estoque de Capital
Essa é uma definição polêmica. Muitos teóricos divergem sobre o que seja "capital" e mais ainda sobre o que seja "estoque de capital", mas podemos aqui humildemente resumir esses conceitos da seguinte forma:
a) Em crescimento econômico, é comum a definição de capital como estoque final de produção disponível a uma firma ou uma economia em determinado ponto no tempo. Observe que não estamos incluindo assim terra nem direitos de propriedade. Embora pareça irreal essa definição, um considerável número de análise em teoria do crescimento tem mostrado que esses outros conceitos de capital realmente podem ser relevados quando se analisa crescimento econômico. No entanto, para outras análises em teoria econômica, recomenda-se que não se negligencie esses fatores. É importante notar que quando tratamos de capital exclusivamente como objetos físicos, definimos por tabela, o Investimento Líquido como o fluxo de novas máquinas que aumentam esse estoque.
b) É comum desde poucos anos atrás se observar a extensão do conceito de capital a aspectos como infraestrutura geral (capital social) e aos talentos e aptidões de uma população (capital humano). De maneira que gastos do governo em educação por exemplo entram como investimento. Essa visão é praticamente indiscutível, mas é controversa ainda a maneira como ela entra na contabilidade social. Sendo assim, quando necessário, distinguiremos aqui entre as duas coisas.
c) Algumas vezes (principalmente nos cursos de administração e contabilidade), o termo capital é usado como referência à soma financeira utilizada para iniciar um investimento e para uma expectativa de lucros. Neste sentido, para a teoria do crescimento econômico, o termo não será usado. Aliás, é bom dizer que o chamado "investimento em bolsas de valores" não é um investimento no sentido econômico, pois não gera nova adição líquida ao estoque de capital da firma ou da economia como um todo. Portanto, investimento aqui nesse texto, se referirá somente à aspectos físicos (mesmo que quando referir-se a capital humano, pois se precisará de novas escolas e estruturas por exemplo).
Posto isto, fica claro que a definição "a" deverá ser a mais usada ao longo de um texto sobre crescimento econômico. A questão então passa a ser como conceituaremos o estoque total de capital de uma economia. Ou seja, mesmo que consideremos máquinas, imóveis e equipamentos exclusivamente como capitais, como podemos somá-los de maneira homogênea dentro de uma economia? A resposta comum seria dizer que devemos somá-los pelo seu valor financeiro. Mas se fosse simples assim, estaríamos eliminando do capital a sua principal características, a de gerar mais capital! (e toda a teoria econômica praticamente pra nada seriviria...). Logo, uma maneira conveniente de se fazer tal soma é pelo Valor Presente desses objetos, para podermos assim considerar o lucro que cada máquina dá ou vem a dar a seus proprietários.
Embora ganhemos em precisão de definição definindo essa soma pelo valor presente de cada objeto, ganhamos um pouco em complexidade na medida que o cálculo do valor presente trás algumas variáveis novas para a questão, aos quais não nos prenderemos nesse momento. Mas fica a definição metodológica pra quando for necessária. Por fim, utilizaremos a notação comum K para quando formos nos referirmos a Capital.
c) Estoque de Trabalho
Essa definição é um pouco mais simples. Logicamente existem diversos tipos de trabalho, mas para o que tange à teoria do crescimento econômico, trataremos de assumir uma força de trabalho homogênea. De maneira a medir tal estoque em termos de de homens-hora. Tomaremos também a força de trabalho como uma proporção fixa da população total (o que não inviabiliza nossa breve análise do gráfico na figura 1 deste texto). Ou seja, L = aP, onde L = força de trabalho, P = população e a é uma constante. Dessa maneira, mais adiante assumiremos que a força de trabalho cresce à mesma taxa que a população P (ou seja, se considerará que a força de trabalho cresce a uma taxa constante e exógena). Dessa maneira, mecanismo malthusianos por exemplo são ignorados.
É claro que essas simplificações são questionáveis, mas essas são necessárias para a construção inicial do modelo. Na medida em que for possível o relaxamento das hipóteses, essas obstruções irão surgir dentro das nossas análises.
Colocadas essas categorias, sigamos adiante. O estudante deve atentar que a teoria do crescimento econômico usará muitas formas de agregação e parábolas para construir suas colocações (por exemplo, quando se usa a parábola de que a economia produza um único bem). Mas é importante notar que essas alusões fictícias não retiram a generalidade dos modelos, e que portanto podem ser usadas.
Agora observe que na economia algumas condições de equilíbrio tradicionais (básicas nos livros de macroeconomia) devem existir. A primeira dessas igualdades, é a equidade entre oferta e demanda. Em qualquer mercado, a quantidade realmente ofertada em qualquer período de tempo deve ser igual à quantidade realmente comprada, já que toda compra corresponde a uma venda. O aparato das curvas de oferta e demanda, entretanto, refere-se a planos de compras e vendas a diferentes preços - sendo o preço de equilíbrio determinado pela igualdade entre oferta planejada e demanda planejada. Assim, se escrevermos D = demanda e S = oferta, usamos o subscrito A para indicar valores efetivos; a afirmação:
é fundamentalmente diferente da afirmação:
D = S
A primeira identidade expressa o fato de que, no sentido contábil, oferta e demanda efetivas devem ser iguais, enquanto que a segunda é a condição de equilíbrio para um mercado competitivo. no contexto do modelo macroeconômico, o investimento efetivo deve igualar a poupança efetiva como uma simples consequência dos métodos convencionais de contabilidade nacional. Por outro lado, o investimento planejado não precisa igualar a poupança planejada. A intersecção das curvas de poupança planejada e investimento planejado determina o nível de equilíbrio da renda nacional num modelo macroeconômico keynesiano simples. Alguns escritores utilizam os termos ex-ante e ex-post para distinguir entre quantidades planejada e efetivas. Assim, nessa terminologia, a poupança ex-post deve igualar o investimento ex-post, enquanto a igualdade de poupança e do investimento ex-ante é condição de equilíbrio do modelo macroeconômico simples.
Estas distinções aparecem e reaparecem em muitas instâncias na análise do crescimento econômico. Assim sendo, caso você não confie nelas, é bom dar uma olhada nos livros de macroeconomia básica.
Poupança e Investimento
Todo modelo de crescimento econômico passa pela noção de poupança e investimento, assim como quase todo modelo macroeconômico. Logicamente, torna-se crucial a sua compreensão. Basicamente, os modelos simples de crescimento adotam a poupança agregada como uma função simples do nível de renda Y: S = s(Y), onde S = poupança agregada e Y = o nível de renda. Apesar do aparecimento de teorias de poupança mais sofisticadas², muitas das teorias de crescimento continuam supondo que a poupança agregada é proporcional à renda agregada:
S = sY
onde s corresponde tanto à propensão marginal quanto à média à poupar. Esse índice é tomado como positivo porém menor que 1, (0 < s < 1), o que claramente quer dizer que uma parte, e não toda renda, é destinada à poupança. Gráficamente, seria algo como a figura 2:
Figura 2 - Propensão Média e Marginal a Poupar
As novas formulações a cerca da poupança são bastante úteis, mas a sua forma simplificada como a que apresentamos aqui é também notadamente útil. Além dessa formulação apresentada, também podemos construir derivações da poupança no contexto do crescimento econômico, que envolvam sua divisão entre renda de salário e renda de lucro. Nessa versão, a função poupança agregada tomaria a seguinte forma:
S = swW + spP com Y = W + P
e 0 < sw < sp < 1
onde
W = renda de salários, P = lucros
sw = propensão a poupar dos salários
sp = proprensão a poupar dos lucros
Essa é uma versão kaleckiana (Kalecki) conhecida como função clássica da poupança, e envolve a hipótese de uma propensão marginal a poupar dos salários igual a zero:
S = spP com 0 < sp <>
Torna-se claro que em ambos os casos, a propensão marginal a poupar da economia depende da distribuição da renda entre salários e lucros.
Nível de Investimento
Dois conceitos básicos de investimento tendem a se mostrar importantes em análises de crescimento: o modelo keynesiano do multiplicador e o conceito mais antigo de acelerador - que é um caso particular da idéia geral de um FUNÇÃO DE INVESTIMENTO.
a) O Multiplicador
Se você já estudou algo em macroeconomia deve estar familiarizado com o coneito de multiplicador, no qual um aumento do investimento tende a aumentar o produto agregado dentro uma dada proporção. Caso não o tenha feita, aqui será feita uma breve apresentação:
Considerando a igualdade entre poupança e investimento:
Nível de Investimento
Dois conceitos básicos de investimento tendem a se mostrar importantes em análises de crescimento: o modelo keynesiano do multiplicador e o conceito mais antigo de acelerador - que é um caso particular da idéia geral de um FUNÇÃO DE INVESTIMENTO.
a) O Multiplicador
Se você já estudou algo em macroeconomia deve estar familiarizado com o coneito de multiplicador, no qual um aumento do investimento tende a aumentar o produto agregado dentro uma dada proporção. Caso não o tenha feita, aqui será feita uma breve apresentação:
Considerando a igualdade entre poupança e investimento:
I = S
Isso implicaria que I = sY
Considerando um aumento de  em I. Isso gera qualquer incremento
em I. Isso gera qualquer incremento  em Y:
em Y:
As opções que Jones apresenta para esta controvérsia, num nível teórico, é: considerar por meio de uma simplificação draconiana que poupança é igual a investimento ex-ante (e pronto!), ou considerar, por uma forma não menos simplificadora, que haja uma entidade (talvez o governo), que "force" a S ser igual a I ex-ante. A princípio, não precisaremos usar estas simplificações para nossas construções de modelos para crescimento. De qualquer forma, ficam aqui apresentadas.
 em I. Isso gera qualquer incremento
em I. Isso gera qualquer incremento  em Y:
em Y:Então a relação entre o aumento em Y e o aumento em I é dado por 1/s. Desde que 0 < s < style="font-style: italic;">I gera um incremento maior em Y.
b) Função Investimento e o Princípio do Acelerador
A proposta keynesiana de interpretação da poupança e do investimento implica em uma consideração de equidade entre uma coisa e outra ex-post, ou seja, mesmo que a decisão de poupar e investir seja tomada por agentes diferentes, no média prazo, os montantes devem ser iguais. No entanto, exatamente por serem decisões tomadas por sujeitos diferentes (ou geralmente diferentes), a poupança e o investimento ex-ante não precisam necessariamente serem iguais.
b) Função Investimento e o Princípio do Acelerador
A proposta keynesiana de interpretação da poupança e do investimento implica em uma consideração de equidade entre uma coisa e outra ex-post, ou seja, mesmo que a decisão de poupar e investir seja tomada por agentes diferentes, no média prazo, os montantes devem ser iguais. No entanto, exatamente por serem decisões tomadas por sujeitos diferentes (ou geralmente diferentes), a poupança e o investimento ex-ante não precisam necessariamente serem iguais.
As opções que Jones apresenta para esta controvérsia, num nível teórico, é: considerar por meio de uma simplificação draconiana que poupança é igual a investimento ex-ante (e pronto!), ou considerar, por uma forma não menos simplificadora, que haja uma entidade (talvez o governo), que "force" a S ser igual a I ex-ante. A princípio, não precisaremos usar estas simplificações para nossas construções de modelos para crescimento. De qualquer forma, ficam aqui apresentadas.
O princípio do acelerador se baseia na hipótese de que o investimento líquido programado pelos empresários seja concebido com base na demanda agregada que esses próprios empresários criariam, que em si, é a própria renda nacional Y. Assim sendo, o investimento líquido estaria associado a aumentos de nível da renda nacional.
De maneira simples, podemos escrever o princípio do acelerador como:
Ou seja, o investimento líquido de um dado período, It, seria dependente de uma proporção fixa v (coeficiente acelerador), da diferença entre a demanda por produto no período t, Yt, e a demanda por produto no período anterior, Yt-1.
Mas observe que estamos tratando de expectativas, e talvez seja insensato adota-las como correspondentes diretos da realidade, afinal, nem sempre a demanda se comportará como esperam os empresários (e provavelmente nunca será "exatamente" como eles imaginam). Dessa forma, talvez seja mais conveniente tratarmos tal produto (do tempo presente), como uma expectativa.
Ou seja, o investimento líquido continua dependendo do mesmo coeficiente acelerador v, mas que agora multiplica a diferença entre o produto esperado do período atual e o produto do período anterior (esse sim, é concebível que seja conhecido).
Se você observar atentamente provavelmente encontrará uma série de pontos questionáveis nesse princípio do acelerador, mas ele passou por algumas reformulações que o arrumaram para que depois ele se encaixasse melhor na teoria macroeconômica. Ainda assim, ele é uma ferramenta preterida. Um princípio semelhante que dele foi gerado, foi o princípio de ajustamento do estoque de capital (A.E.C.), de autoria de Matthews, que sugere que o volume de investimento varia diretamente com o nível da renda nacional e inversamente com o estoque de capital já em existência. Assim, uma versão linear, incorporando expectativas, desse princípio pode ser escrita.
que tem uma simbologia óbvia. Jones (1975) levanta o questionamento se algum desses princípios são "racionais" para o empresário individual.
De qualquer forma, a versão mais aceita dos determinantes do invetimentos é a que relaciona o nível de investimento à taxa de juros. seja se considerarmos a taxa interna de retorno, seja se considerarmos o valor presente. De qualquer forma, não serão muitas vezes que a especificação profunda do investimento seja necessária para uma boa teoria do crescimento econômico, a não ser que se esteja num nível de profundidade teórica bem acima do qual esse texto se propõe a ter.
A Tecnologia da Economia
É uma afirmação razoavelmente óbvia de que o produto de uma determinada economia é limitado pela quantidade disponível de capital e de trabalho. É relação lógica entre produto e insumos. Esse tipo de relação pode ser colocada no que comumente se conhece como função de produção agregada
Y = F(K,L)
onde estamos afirmando que o produto agregado Y, é uma função da quantidade de capital K, e da quantidade de trabalho L, que se disponha nessa economia. Não nos aprofundaremos nos pormenores dessa hipótese sobre a produção genérica, mas o leitor mais receoso poderá encontrá-la em qualquer livro de graduação tanto de micro quanto de macroeconomia. No geral, nos ateremos a duas formas específicas de de produção que tendem a serem úteis para análises de crescimento: a forma de coeficientes fixos e a forma contínua.
Coeficientes Fixos
Essa interpretação da função de produção estima que, dado qualquer estoque de capital particular, existe um e somente um fluxo de produto que pode ser gerado - e similarmente para qualquer estoque de trabalho dado. Mais ou menos produto seria obtido somente por um ajuste que mantenha a proporção entre capital e trabalho. Escreveríamos essa função como:
Onde v e u são constantes, que simbolizam a restrição à qual o capital e o trabalho estão sujeitos. Torna-se claro que na função acima, estamos escolhendo que for menor k/v ou L/u. Esta condição implica que se tivermos um produto específico para uma condição mínima de capital K ou trabalho L, então não adiantaria aumentar a quantidade do outro fator que está em maioria, pois nesse caso, o produto permaneceria o mesmo. Teríamos assim uma condição do ociosidade, ou do capital ou do trabalho. Essa forma permite a substituição de capital agregado por trabalho na produção de bens. Assim, qualquer fluxo dado de produto Y pode ser produzido por uma variedade de combinações de capital e trabalho.
Com a forma contínua da função de produção agregada, é possível discutir o efeito sobre o produto total de um incremento marginal de capital ou de trabalho. Definimos produto marginal do trabalho como o produto adicional gerado por um incremento na força de trabalho (ou oferta de serviços da mão-de-obra), com o estoque de capital mantido constante. Esse conceito se mostrará crucial ao longo dos seus estudos a cerca do crescimento econômico.
De maneira mais analítica, podemos dizer que o produto marginal do trabalho é a taxa de mudança do produto, Y, com respeito a uma mudança no trabalho L, e utilizamos a notação diferencial para denotá-lo,  , isto é, a derivada parcial do produto em relação ao trabalho. O produto marginal do capital por analogia será
, isto é, a derivada parcial do produto em relação ao trabalho. O produto marginal do capital por analogia será 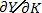 , e denotará a variação no produto dado alterações no capital e manutenção constante do trabalho.
, e denotará a variação no produto dado alterações no capital e manutenção constante do trabalho.
 , isto é, a derivada parcial do produto em relação ao trabalho. O produto marginal do capital por analogia será
, isto é, a derivada parcial do produto em relação ao trabalho. O produto marginal do capital por analogia será 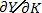 , e denotará a variação no produto dado alterações no capital e manutenção constante do trabalho.
, e denotará a variação no produto dado alterações no capital e manutenção constante do trabalho.Feito isso, assumiremos ainda que os produtos marginais são positivos. Ou seja, alterações positivas de capital ou trabalho sempre acrescentam algo ao fluxo de produto, mesmo que minimamente. Em forma diferencial, estamos dizendo que,
Observe que aqui estamos fugindo da hipótese comum na microeconomia na qual depois de certo ponto, acréscimos de insumos chegam a reduzir a produção. Aqui, isto nunca aconteceria.
Consideraremos também que a produtividade marginal é decrescente. Ou seja, mesmo que qualquer incremento de capital ou trabalho acarrete em aumento do fluxo de produto, assumiremos que esse aumento será cada vez menos, ou seja, sucessivos aumentos em capital ou trabalho produzem incrementos decrescentes no fluxo de produto. Em termos diferenciais,
Aqui há novamente uma alteração em relação a uma concepção comum da microeconomia. Lá, é comum que rendimentos decrescentes surjam apenas depois de algum determinado ponto da produção. Aqui, assumiremos que retornos decrescentes se apresentem em todo o campo de variação do produto.
Assumiremos também que há homogeneidade linear ou retornos constantes de escala. Não confunda com a hipótese anterior de retornos decrescentes. Antes assumimos que acréscimos de capital ou trabalho acarretem aumentos cada vez menores de fluxo de produto, dado que a outra variável permaneça constante. Agora, ao colocarmos o termo "de escala" na expressão depois de retornos constantes, estamos assumindos que a função de produção responde de maneira proporcional a aumentos "em ambos" insumos simultaneamente. Ou seja, se dobrarmos a quantidade de capital e trabalho, dobraremos o produto. Diz-se que uma função de produção é linearmente homogênea, isto é, opera sujeita a retornos constantes de escala, se a multiplicação de ambos, capital e trabalho por um número positivo implica que o produto gerado seja multiplicado pelo mesmo número
Essas hipóteses que aqui colocamos serão muito frequentemente utilizadas em estudos futuros referentes à teoria do crescimento econômico. Sendo assim, é importante que as tenha entendido bem. Essa última função de retornos constantes de escala permitirá uma simplificação bastante útil na análise das funções de produção agregada, já que poderemos escrevê-la na forma por trabalhador ou na forma "intensiva". Ou seja, se multiplicarmos agora Y = F(K, L) por 1/L, dado que temos retornos constantes de escala, obtemos:
Y/L = F [K/L , 1]
O que esta última equação está afirmando é que o produto por trabalhador, Y/L dependerá do capital por trabalhador Y/L (as vezes também conhecido como relação capital-trabalho). Poderemos então adaptar a nossa notação, de maneira que simplesmente escreveremos (como é costume nos livros da área):
y = f(k)
onde y = Y'/L', k = K/L e f (k) = F (k, 1)
Essa equação formada por letras minúsculas em itálico é muito usada em modelos de crescimento. Agora, acrescentando mais uma hipótese, poderemos já colocar a função de produção num gráfico. Assumiremos que não haverá produto sem insumo. Afinal, se nenhum capital ou trabalho é empregado, entendemos que não haverá nenhum produto a ser produzido por impossibilidade física, isto é, dado y = f(k), se k = 0, então y = 0.
Com isso, podemos construir o gráfico da figura 3:
Figura 3
Estamos assegurados pelas hipóteses de que a relação inicia-se em (0,0), de que a declividade é positiva e de que a inclinação se reduza gradativamente mas sempre mantendo-se positiva.
Agora podemos ir um pouco além e pensar nos pormenores desta relação. De início podemos averiguar que existe uma coisa chamada "teoria da distribuição segundo a produtividade marginal", que irá nos colocar que a taxa de salário real do trabalho irá igualar ao produto marginal do trabalho como um todo e que o aluguel real para uma unidade do capital será igualado ao produto marginal como um todo. Isto é um resultado semelhante ao que encontramos na microeconomia ao que encontramos na microeconomia quando dizemos que um empresário maximizará seu lucro quando a receita marginal do produto igualar seu preço (e até então, ele continuará contratando mais mão-de-obra. No caso da macroeconomia, sugere-se que os retornos do capital se igualem aos retornos do trabalho no ponto ótimo. Esta é uma concepção neoclássica (e como você deverá perceber, um tanto ingênua).
Logicamente, se isto ocorresse com exatidão na realidade geraria uma lógica de distribuição de renda muito mais adequada, mas é fácil perceber que isso não ocorre. Vejamos isto matematicamente... Considerando, pela definição de derivada, que o produto marginal do capital, 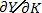 medida num ponto é igual à reta tangente à esse ponto, e se a teoria da produtividade marginal for aceita, a mesma tangente medirá a taxa de lucro ou a taxa de aluguel do capital, que seria gerada por condição competitivas, dada uma quantidade do capital K*. Considere a figura 4:
medida num ponto é igual à reta tangente à esse ponto, e se a teoria da produtividade marginal for aceita, a mesma tangente medirá a taxa de lucro ou a taxa de aluguel do capital, que seria gerada por condição competitivas, dada uma quantidade do capital K*. Considere a figura 4:
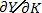 medida num ponto é igual à reta tangente à esse ponto, e se a teoria da produtividade marginal for aceita, a mesma tangente medirá a taxa de lucro ou a taxa de aluguel do capital, que seria gerada por condição competitivas, dada uma quantidade do capital K*. Considere a figura 4:
medida num ponto é igual à reta tangente à esse ponto, e se a teoria da produtividade marginal for aceita, a mesma tangente medirá a taxa de lucro ou a taxa de aluguel do capital, que seria gerada por condição competitivas, dada uma quantidade do capital K*. Considere a figura 4:Figura 4
Dada a relação capital/trabalho k*, um produto por trabalhador é produzido y*. Pelo argumento do parágrafo anterior, não é difícil aceitar que a inclinação da tangente no ponto A mede o produto marginal do capital naquele ponto e, se a teoria da distribuição segundo a produtividade marginal for aceita, essa inclinação será igual a à taxa de lucro r. Essa mesma inclinação é dada por CD/DA: isto é, a inclinação da tangente
CA = r = CD/DA
Mas como DA é igual a OE que é a relação capital/trabalho, k*, associada à tangente CA, teremos que
r = CD/OE = CD/k*
ou CD = rk*
Observe que rk* é a taxa de lucro multiplicada pelo montante de capital por trabalhador. Sendo assim, teremos que CD será a medida da quantidade de lucros por trabalhador. Uma vez que OD mede o montante total de produto por trabalhador e assume os retornos constante de escala, implicando a exaustão do produto, os salários por trabalhador, ou a taxa de salário, serão dados por
Salário por Trabalhador = OD - CD
= OC
Esse é um resultado importante. O grau de inclinação da função de produção intensiva em um ponto é frequentemente denotado como f' (k). Assim, dada uma relação capital/trabalho de k* , a taxa de lucro r será muitas vezes escrita como
r = f '(k*)
O lucro por trabalhador será, portanto, igual a k*f '(k*) e salários por trabalhador, w, será dado nessa notação por
w = produto por trabalhador - lucro por trabalhador
= f (k*) - k*f '(k*)
Por fim, observe que a inclinação da tangente CA pode ser escrita de forma alternativa
Inclinação de CA = r = OC/OB
Tendo demonstrado que OC mede a taxa de salário, w. Então
r = w/OB
OB = w/r
De tudo isso, cabe-nos resumir o que foi dito nessa breve digressão algébrica, que analisa graficamente a associação da função contínua de produção por trabalhador com a hipótese da produtividade marginal em três pontos:
1. Lucros por trabalhador são medidos pela distância CD;
2. Salários por trabalhador são medidos pela distância OC;
3. A relação entre salários por trabalhador, w, e taxa de lucro, r, é medida pela distância OB.
Passemos então para um outro conceito, o de elasticidade de substituição.
Esse conceito, tão útil em várias frentes da teoria econômica, pode ser caracterizado como a taxa proporcional de mudança da relação entre uma determinada variável e outra, geralmente feita sob condições percentuais. No caso, se referiria à taxa proporcional de mudança da relação entre capital e trabalho em relação à mudança na razão dos preços de capital e trabalho. Pode parecer um pouco confuso, mas podemos desenvolver um raciocínio mais claro a respeito.
Como demonstramos anteriormente, a relação entre salários por trabalhador e a taxa de lucro pode ser medida por OB na figura 4. Consideremos o efeito sobre a relação capital/trabalho de uma variação na distância OB enquanto a linha AB é mantida tangente à curva f (k). Uma relação capital/trabalho maior será associada a um aumento na distância OB, isto é, um k maior será associado a uma valor maior de w/r. Similarmente, uma relação capital/trabalho menor será associada a uma redução nessa distância OB - isto é, um k menor associado a um menor valor de w/r. Deve estar claro então que a relação capital/trabalho é uma função da relação salário/taxa de lucro:
k = F (w/r)
ou, invertendo w/r,
k = F (r/w)
Assim, pelo o que conversamos antes, quando r/w cresce (e w/r decresce), a relação capital/trabalho, k, decresce. Essa relação pode ser vista na figura 5. A elasticidade de substituição poderá simplesmente ser definida pela curva AA (na literatura ela costuma receber outras designações, mas isso não importa tanto aqui).
Figura 5
Utilizando a metodologia de Jones (1975), onde,
E como a curva AA tem inclinação negativa, a definição de elasticidade de substituição na última equação terá uma definição inerentemente negativa. Por convenção, o sinal é muitas vezes invertido.
Assim, a elasticidade faz-se por seu conceito, ou seja, mede a sensibilidade da relação entre capital/trabalho aos preços do capital e do trabalho. Se tal sensibilidade for igual a zero, então é claro que a relação capital/trabalho é totalmente insensível a qualquer mudança r/w, isto é, não há possibilidade (tanto tecnicamente quanto pelas preferências dos empresários) de substituir capital por trabalho. Se, por outro lado, a elasticidade de substituição for igual a um, então, uma pequena queda na relação r/w seria associada a um aumento semelhante e proporcional na relação capital/trabalho.
Formas Alternativas de Apresentação das Funções de Produção Contínuas
A Cobb-Douglas
Esta é provavelmente a forma mais consagrada de apresentação de uma função de produção. Ela é reconhecida pela seguinte forma escrita
onde, se a + b = 1, então a função de produção estará apresentando retornos constantes de escala, e poderá ser escrita como
Onde, se forem feitas as devidas contas, poderá se observa que a elasticidade de substituição entre os fatores é constante.
A E.S.C.
Esta função conhecida pela sua sigla é simplesmente uma função de elasticidade de substituição constante que em sue forma mais simples é dada por
Alem de tudo isso, antes de entrarmos especificamente nos modelo de crescimento econômico, é interessante que você tenha algum domínio sobre derivadas e taxas de crescimento. Se você se sentir bem quanto a isso pode seguir em frente, se não, escrevemos um blog especialmente para você em http://derivadasetaxasdecrescimento.blogspot.com/ e a sua continuação para uma análise um pouco mais aprimorada em http://taxasdecrescimentoelogaritmos.blogspot.com/ .
Ok. Feito tudo isso você está pronto para entrar nas teorias a cerca do crescimento econômico. Deu trabalho? Com certeza! Mas se você chegou até aqui na sua leitura é porque você não é um simples estudante, mas alguém que busca o conhecimento e faz a diferença nesse mundo hipercompetitivo. Então eu te convido a continuar conosco e analisar o modelo de Harrod-Domar, a base para a construção do Modelo de Solow-Swan e os demais que o seguem.
Basicamente, nós construiremos a idéia do que seja crescimento equilibrado e principalmente, à longo prazo. E buscaremos identificar respostas para perguntas como a que foi feita anteriormente neste texto para a comparação ente o crescimento chinês e o brasileiro. Veremos que a análise do que seja um estado estável de crescimento, ou seja, condições nas quais o capital e o trabalho cresçam a mesmas taxas, é uma boa parábola para construção de modelo sofisticados de análise.
Seja então bem-vindo ao nosso próximo blog:
O MODELO DE HARROD-DOMAR
¹Nota do Blog
²Como as de Friedman e Modigliani, e Brumberg e Ando por exemplo.
imagem fonte: http://blogdofavre.ig.com.br/tag/des/





.bmp)









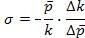
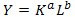


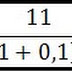


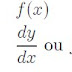


Nenhum comentário:
Postar um comentário